티스토리 뷰
안녕하세요. 은행 IT운영부 이지성과장입니다.
코로나 바이러스가 3월에 더욱 기승을 부리고 있습니다.
머신러닝에 대한 흥미로운 기사를 보아서 소개해드리려 합니다. 코로나 관련 데이터를 기반으로 하여 "발병 예측 모델"을 국내의 한 대학원생이 만들어 배포하였다고 합니다. 머신러닝이 의학 및 의료 관련 정책에도 많이 사용될 수 있다는 가능성을 보여주는 대목인 것 같습니다. (데이터는 거짓말을 안하니까요 ^0^;;;)
링크 : https://m.etnews.com/20200306000213
韓 대학원생 '코로나 예측 데이터셋' 세계 배포
코로나19 확산을 막기 위해 데이터가 활용된다. 데이터를 투입해 인공지능(AI) 기술로 코로나19 확진자와 사망자를 예측한다. 특히 데이터 원재료를 한국 대학원생이 만들어 세계에 배포한다. 기계학습 기반의 예측...
www.etnews.com
오늘은 분류 알고리즘 중 가장 가시적으로 데이터를 볼 수 있는 의사결정나무 (Decision Tree)에 대해서 알아보겠습니다.

데이터 구조에서 "트리 구조"는 학부 시절 많이 들어보셨을 거라 생각합니다.
부모 노드, 자식 노드 , 레벨 등 트리구조는 개발자라면, 생소하지 않은 개념이라고 생각되는데요.
의사결정나무에서도 이와 비슷하게 상위 노드에서 하위 노드로 데이터를 분류해가며, 전체의 자료를 몇 개의 소집단으로 분류하는 그런 알고리즘 이라고 할 수 있습니다.

의사결정나무의 경우 여러가지 장점이 있는데,
1) 분류가 되는 의사결정 과정을 시각적으로 보여주어, 데이터 해석이 용이합니다.
2) 숫자형, 범주형 데이터에 모두 사용할 수 있는 기법입니다. (분류와 회귀가 모두 가능합니다)
3) 데이터에 결측값이 있더라도 사용가능하며, 대규모의 데이터에도 분석이 가능합니다.
그러나 의사결정나무의 단점은, 모델이 과적합 (over-fitting) 될 수 있는 가능성이 큰데,
과적합이란, 모델에서 훈련된 데이터로는 분류 결과가 좋았으나, 실제 데이터로 모델을 통해 예측하였을 경우,
성능이 좋지 않은 현상을 말합니다.
그리하여, 이런 의사결정나무의 단점을 보완하기 위해 "앙상블" 기법을 많이 사용하는데,
앙상블 기법에 대한 내용을 아래 링크를 참고하시고, 별도의 주제로 한번 다루도록 하겠습니다.
앙상블기법 LINK : https://blog.naver.com/rek0822/221355769780
머신러닝알고리즘(의사결정나무, 앙상블 기법)
0.이번 포스트에서는 의사결정트리와 앙상블 기법을 다룬다. 랜덤 포레스트와 앙상블 기법은 아주 중요한데...
blog.naver.com
이제 의사결정나무 코딩을 시작해보도록 하겠습니다. 데이터는 k-nn때 사용한 데이터인 붓꽃데이터(iris) 데이터를 사용하도록 하겠습니다. 추가로 지난번 먼저 소개해드린 k-nn 알고리즘과 비교하여 의사결정나무와 k-nn 알고리즘 중 어떤 알고리즘이 더 성능이 좋은지도 마지막으로 살펴보도록 하겠습니다.
<코딩>
#라이브러리 호출
library(rpart)
#데이터셋
iris_data <- iris
#seed 생성
set.seed(123)
#샘플 키값 저장
idx <-sample(1:nrow(iris_data),0.7*nrow(iris_data))
idx
#7:3비율로 분리
iris_train <- iris_data[idx,]
iris_predict <- iris_data[-idx,]
#데이터확인
head(iris)
# Sepal.Length Sepal.Width Petal.Length Petal.Width Species
#1 5.1 3.5 1.4 0.2 setosa
#2 4.9 3.0 1.4 0.2 setosa
#3 4.7 3.2 1.3 0.2 setosa
#4 4.6 3.1 1.5 0.2 setosa
#5 5.0 3.6 1.4 0.2 setosa
#6 5.4 3.9 1.7 0.4 setosa
#모델생성
#Species 를 종속변수, ~ 나머지 모든 변수를 독립변수로
#data=iris 데이터를 사용
Treemodel <- rpart(Species~. , data= iris_train)
#모델확인
Treemodel
#n= 105
#
#node), split, n, loss, yval, (yprob)
# * denotes terminal node
#
#1) root 105 67 setosa (0.3619048 0.3142857 0.3238095)
# 2) Petal.Length< 2.6 38 0 setosa (1.0000000 0.0000000 0.0000000) *
# 3) Petal.Length>=2.6 67 33 virginica (0.0000000 0.4925373 0.5074627)
# 6) Petal.Length< 4.75 29 0 versicolor (0.0000000 1.0000000 0.0000000) *
# 7) Petal.Length>=4.75 38 4 virginica (0.0000000 0.1052632 0.8947368) *
#결과를 도표로 생성
plot(Treemodel, margin=.1)
text(Treemodel, cex=1)
#predict 데이터로 예측하기
predict(Treemodel, newdata=iris_predict, type = "class")
2 4 10 13 19 21
setosa setosa setosa setosa setosa setosa
22 31 32 41 42 49
setosa setosa setosa setosa setosa setosa
51 52 58 59 62 63
versicolor versicolor versicolor versicolor versicolor versicolor
67 72 76 78 81 84
versicolor versicolor versicolor virginica versicolor virginica
88 91 96 98 99 102
versicolor versicolor versicolor versicolor versicolor virginica
103 105 107 109 110 117
virginica virginica versicolor virginica virginica virginica
120 125 129 133 136 140
virginica virginica virginica virginica virginica virginica
141 144 149
virginica virginica virginica
Levels: setosa versicolor virginica
#성능평가
library(gmodels)
predict_result <- predict(Treemodel, newdata=iris_predict, type = "class")
CrossTable(x = iris_predict$Species, y=predict_result, prop.chisq = F)
| predict_result
iris_predict$Species | setosa | versicolor | virginica | Row Total |
---------------------|------------|------------|------------|------------|
setosa | 12 | 0 | 0 | 12 |
| 1.000 | 0.000 | 0.000 | 0.267 |
| 1.000 | 0.000 | 0.000 | |
| 0.267 | 0.000 | 0.000 | |
---------------------|------------|------------|------------|------------|
versicolor | 0 | 15 | 2 | 17 |
| 0.000 | 0.882 | 0.118 | 0.378 |
| 0.000 | 0.938 | 0.118 | |
| 0.000 | 0.333 | 0.044 | |
---------------------|------------|------------|------------|------------|
virginica | 0 | 1 | 15 | 16 |
| 0.000 | 0.062 | 0.938 | 0.356 |
| 0.000 | 0.062 | 0.882 | |
| 0.000 | 0.022 | 0.333 | |
---------------------|------------|------------|------------|------------|
Column Total | 12 | 16 | 17 | 45 |
| 0.267 | 0.356 | 0.378 | |
---------------------|------------|------------|------------|------------|
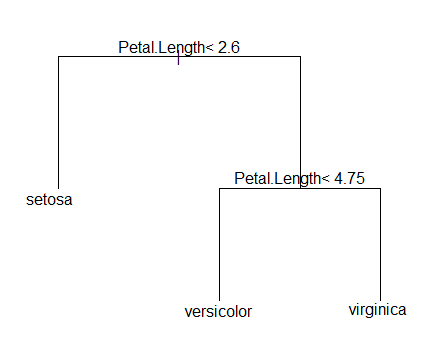
<의사결정나무>
첫번째 분류(노드)로 Petal.Length의 수치가 2.6을 기준으로 setosa와 아닌 것을 분류를 하고 있습니다.
Petal.Length의 수치 2.6 보다 작으면 우선적으로 setosa로 분류하고 있네요.
두번째 분류(노드)로 Petal.Length의 수치가 4.75를 기준으로 versicolor와 virginica를 분류하고 있습니다.
<결과확인>
predict 데이터를 모델에 입력시켜 결과를 얻었습니다.

<k-nn과 비교>
1. k-nn

2. decision tree

오분류는 모두 45건 중 3건으로 두 알고리즘의 성능은 비슷...해 보입니다..쿨럭 ;;
예측 샘플이 더 많았다면 다른 결과가 있을 수도 있겠죠??
마지막으로 의사결정나무에서 한가지 중요한 부분이 있습니다. 바로 "지니 불순도" 인데요. (알라딘의 지니가 아닙니다. ㅋㅋㅋㅋ) 노드를 나누는 기준에 바로 이 "지니 불순도"를 사용하게 됩니다. 불순도가 낮다면 분류가 잘 된것이고, 불순도가 높다면 분류가 잘 되지 않았다는 의미로 생각하시면 됩니다. 당연히 의사결정나무는 이 지니 불순도 함수를 사용하여 지니 불순도가 낮은 방향으로 노드 선택의 기준을 잡습니다.
지니 불순도는 통계학적인 지식이 조~~~금 필요하여 아래 링크를 참고하시면 더욱 많은 정보를 보실 수 있습니다.
Decision Tree의 지니 불순도 (Gini Impurity)란 무엇일까? - Small Data Guru
지니 불순도 측정(Gini Impurity Measure)은 Classification Problem에서 사용 가능한 결정 트리(Decision Tree)의 분할 기준 (Split Criteria) 중 하나이다. 첫째, 지니 불순도 측정치가 결정 트리에서 사용되는 방법과는 독립적으로 다양한 각도에서 동기를…
smalldataguru.com
깃허브 LINK : https://github.com/jasonlee8318/R-programming/blob/master/decision-tree.R
다음 주제로는 텍스트를 활용한 여러 머신러닝 기법 (Word2Vec)에 대해서 알아볼 예정입니다.
감사합니다.
*개인적으로 공부한 내용을 정리한 것입니다. 따라서, 오류가 있을 수 있습니다.
너그러운 양해 부탁드리며 댓글 남겨 주시면 해당사항은 수정하도록 하겠습니다.
'data analysis' 카테고리의 다른 글
| cross fold validation 기법 알아보기 (0) | 2020.05.15 |
|---|---|
| 추천시스템 (recommendation system) 이란..? (0) | 2020.03.16 |
| What is EDA(Exploratory Data Analysis)? (0) | 2020.02.25 |
| [regression] linear regression (0) | 2020.02.06 |
| [데이터 시각화] 유용한 사이트 (0) | 2020.01.31 |
- Total
- Today
- Yesterday
- 기술사학원
- 챗봇
- pytorch
- 정보관리기술사합격
- lambda
- wfastcgi
- 머신러닝
- 추천도서
- 추천시스템
- 정보관리
- IIS
- gpt3.5
- FLASK
- 로블록스
- iso12207
- 밀키트
- 12207
- 인조기프
- hackerrank
- 정보관리기술사
- r
- 자기계발
- s3
- 콘도챗봇
- ISO 12207
- AWS
- 131회정보관리기술사
- 밀키트요리
- 기술사
- 정보관리기술사독학
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
